

收稿日期: 2019-03-04
网络出版日期: 2019-04-28
基金资助
国家自然科学基金建设资助项目(11371243);上海市重点学科建设资助项目(S30104);江苏省高等学校自然科学研究面上项目(16KJD110006);常州信息职业技术学院自然科学研究重点项目(CXKZ201908Z)
Parametric greedy randomized Kaczmarz algorithm for solving large sparse linear systems
Received date: 2019-03-04
Online published: 2019-04-28
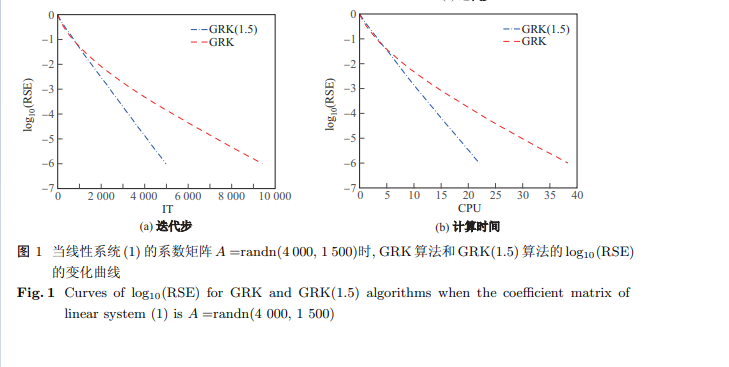
为了求解大型稀疏线性系统, 在贪心随机Kaczmarz (greedy randomized Kaczmarz, GRK)算法的迭代 公式中引入松弛因子,构造了一种含参数的贪心随机Kaczmarz算法.证明了当线性系统相容时该算法的收敛性. 数值实验表明,当选择恰当的松弛因子时, 该算法在迭代步数和计算时间上比贪心随机Kaczmarz算法更有效.
关键词: 大型稀疏线性系统; 贪心随机Kaczmarz算法; 松弛因子
刘永, $\fbox{顾传青}$, 崔蓉蓉 . 大型稀疏线性系统的一类含参数的贪心随机Kaczmarz算法[J]. 上海大学学报(自然科学版), 2020 , 26(6) : 1026 -1034 . DOI: 10.12066/j.issn.1007-2861.2151
To solve large sparse linear systems, a relaxation parameter in introduced in the involved iterative formula of greedy randomized Kaczmarz (GRK) algorithm, and obtain a parametric greedy randomizedKaczmarzalgorithm is obtained. The convergence of this algorithm is proved when the linear system is consistent, and it is showed that it can be more efficient than the greedy randomized Kaczmarz algorithm if the relaxation parameter is chosen appropriately.

| [1] | Kaczmarz S. Angen?herte aufl?sung von systemen linearer gleichungen[J]. Bull Int Acad Polon Sci Lett A, 1937,35:355-357. |
| [2] | Herman G T, Meyer L B. Algebraic reconstruction techniques can be made computationally efficient[J]. IEEE Transactions on Medical Imaging, 1993,12(3):600-609. |
| [3] | Popa C, Zdunek R. Kaczmarz extended algorithm for tomographic image reconstruction from limited-data[J]. Mathematics and Computers in Simulation, 2004,65(6):579-598. |
| [4] | Gordon R, Bender R, Herman G T. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and X-ray photography[J]. Journal of Theoretical Biology, 1970,29(3):471-481. |
| [5] | Byrne C. A unified treatment of some iterative algorithms in signal processing and image reconstruction[J]. Inverse Problems, 2004,20(1):103-120. |
| [6] | Pasqualetti F, Carli R, Bullo F. Distributed estimation via iterative projections with application to power network monitoring[J]. Automatica, 2012,48(5):747-758. |
| [7] | Bai Z Z, Liu X G. On the Meany inequality with applications to convergence analysis of several row-action iteration methods[J]. Numerische Mathematik, 2013,124(2):215-236. |
| [8] | Bai Z Z, Wu W T. On convergence rate of the randomized Kaczmarz method[J]. Linear Algebra and its Applications, 2018,553(15):252-269. |
| [9] | Strohmer T, Vershynin R. A randomized Kaczmarz algorithm with exponential conver-gence[J]. Journal of Fourier Analysis and Applications, 2009,15(2):262-278. |
| [10] | Zouzias A, Freris N M. Randomized extended Kaczmarz for solving least squares[J]. SIAM Journal on Matrix Analysis and Applications, 2013,34(2):773-793. |
| [11] | Bai Z Z, Wu W T. On greedy randomized Kaczmarz method for solving large sparse linear systems[J]. SIAM Journal on Scientific Computing, 2018,40(1):592-606. |
| [12] | Davis T A, Hu Y. The university of Florida sparse matrix collection[J]. ACM Transactions on Mathematical Software, 2011,38(1):1-25. |
/
| 〈 |
|
〉 |